あっぱとっぱな毎日

宿題をやってた娘（小５）が、「『ふりこの長さが2倍になるとふりこの往復時間は2倍になる』って正解？」

と聞いていたので、テキトーに「うん、そうだよね」と答えたんだけど　・・・はて？？　なんかちがうような。

こっそり参考書をのぞいてみると、

「ふりこの往復時間は、ふりこの長さが長いほど長く、短いほど短くなる」

「ふりこの長さを４倍、９倍、１６倍・・・にすると、ふりこの往復時間は２倍、３倍、４倍・・・になる」

・・・だそうです。

こんなこと小学校で覚えたんだっけ？

それにしても、「ふりこの長さを４倍、９倍、１６倍・・・」っていうのがなんだか苦しい。ちょっとゴマカシの匂いがするような。うまい具合に整数比だけで説明しちゃおうという…

「ふりこの長さを2倍、3倍、4倍・・・」って書くと、往復時間は「√2倍、√3倍、２倍」と書くことになっちゃうもんなぁ・・・小学校の算数にルートは出てきちゃだめっていうお約束なのねー、と一人で勝手に納得。

「なんで『４倍、９倍、１６倍・・・』なの？」と娘からつっこまれたら、どうしよう？　とひやひやしたのですが、娘はとにかく早く宿題を終わらせたいらしくて、「ふーん」と答えただけで次の問題へ。

どうして「振り子の長さがn倍になると、周期が√n倍になるのか」って説明は、結構むずかしそう・・高校の物理じゃないとわからないかな？

なにかうまい説明がないもんだろうかと、あれこれ考え中です。

ふりこのGIFを作ってみたけど、うーん、出来がいまひとつ。あとで再チャレンジ。

【追記１】

こんな表が出てきて、長さと周期の関係について考えさせる問題がよくあるみたいなんだけど・・・

25cmと50ｃｍの周期を比べて、1.4倍とはどういうことだー！？　とつめよられそう。

1.4×1.4はだいたい２になるよー、てなことを言ってごまかすしかないのかなー。

（それとも、「そこは見ちゃいかん！」と言う？？　２の平方根の存在を隠そうとしたピタゴラスみたい？）

ほんとは、そういうところから平方根の話とかしたらおもしろそうなんだけど、次々問題を解かなきゃならないから困っちゃう。

【追記2】

ふりこの長さと周期の関係を数式で表すと：（ふり幅が小さいときには）

T = 2π√L/√g　（Tは周期、Lはふりこの長さ、gは重力加速度）

うわあ、だめだこりゃあ。小5は白目をむきそう。。。（私も）

「ふり幅が小さいとき」、っていうのもクセモノだなあ。　たしかにぐるんぐるん振り回したら周期が長くなりそう。でも「小さい」ってどのくらい？

【追記3】

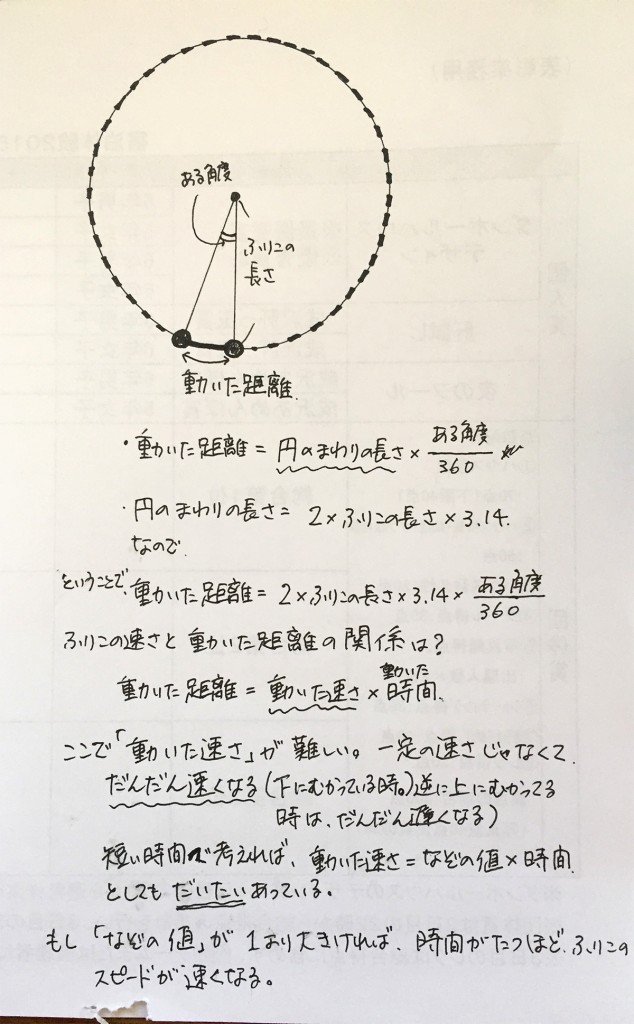
その後も小学生にうまく説明する方法はないものかと考えてメモを作ってみたので、載せてみます。

ふりこの長さを半径にした円で考えると・・・

やっぱり「短い時間で考えると」っていうのが出てきちゃいます（汗

「なぞの値」とか「だいたいあってる」とか、いろいろ苦しいうえに、メモ用紙の下のほうをインコにかじられましたが、めげずに続けます。

なかなか、わかりにくい。。。　重力加速度とかまだわからないし、微分も使えない。

とりあえず、この件はここまで。また何か思いついたら書いてみます。

（良い説明の仕方をご存じの方は教えてください）

インコが見学。

「ナルホド、ぴー」

「あのー、さかさまに読んでますけど・・・」